Pi ile ilgili en iyi bilinen gerçek, normalde 3.14159‘a kadar yuvarlandığı ve bir daire çevresinin çapına olan oranını temsil etmesidir. Pi aynı zamanda mantıksız bir sayıdır, bu yüzden basit bir kesir olarak yazılmaktan acizdir. Bu nedenle pi, insanın bildiği en ilginç ve gizemli sayılardan biri haline getiren, sonsuz uzunlukta, tekrarlanmayan ondalık sayıdır.
İlk Hesaplama
18. yüzyılda Johann Heinrich Lambert pi’nin irrasyonel olduğunu kanıtladı; tam sayıya dayalı bir kesir olarak ifade edilemez. Rasyonel sayılar her zaman hem pay hem de paydanın tam sayı olduğu bir kesir olarak yazılabilir. Pi’yi çevrenin / çapın (pi = C / D) basit bir oranı olarak görmek cazip olsa da , çapın bir tam sayı olması durumunda çevrenin bir tam sayı olmadığı ve tam tersinin durumunun her zaman geçerli olacağı düşünülmektedir .
Bir Dairenin Gerçek Alanı Bilinmiyor
Pi’nin mantıksızlığı, bir dairenin çevresi (ve daha sonra alanını) asla gerçekten bilemeyiz demektir. Bu sinir bozucu ancak görünüşte kaçınılmaz olan gerçek, bazı matematikçilere, bir daireyi “düzgün” olarak düşünürken, bir daireyi sonsuz sayıda köşe olarak düşünmenin daha doğru olduğunu ısrarla öne sürdü.
Buffon İğne
1777’de geometrik ve matematikçilerin ilgisini çeken Buffon’un iğnesi, geometrik olasılık alanında en eski ve en ilginç sorunlardan biridir.
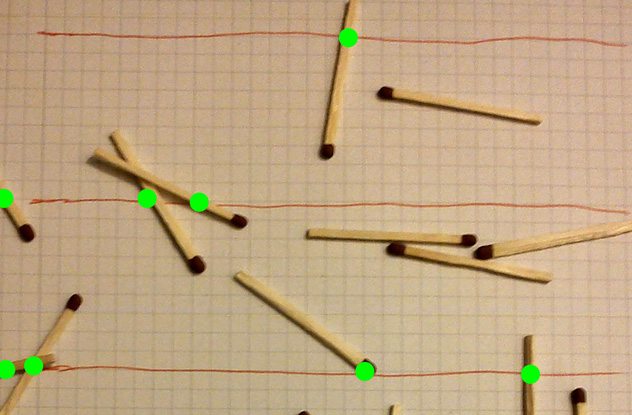
Aynı birim uzunluğa bölünmüş çizgilerle bir kağıt uzunluğuna bir iğne düşürürseniz, iğnenin sayfadaki çizgilerden birinin üzerinde olması olasılığı doğrudan pi’nin değeriyle ilgilidir.
İğne düşmesine ilişkin iki değişken vardır: 1) iğnenin düşme açısı ve 2) iğnenin merkezinden en yakın çizgiye olan uzaklığı. Açı 0 ila 180 derece arasında değişebilir ve kağıttaki çizgilere paralel bir çizgiyle ölçülür.
İğnenin ineceği bir çizgiyi kesebilmesi için tam 2 / pi ya da kabaca yüzde 64 olasılık çıkıyor. Bunun anlamı, deneyin çevrelerle hiçbir ilgisi olmayan ya da bu konuda kenarları yuvarlatılmış gibi görünmesine rağmen, yeterli teorik çalışmalar süresince oturmak için yeterince sabır varsa pi, bu tekniği kullanarak teorik olarak hesaplanabilir demektir.
Pi ve Kurdele Sorunu
Bir kurdeleyi Dünya’ya saracağınızı düşünün. (Sadeliğin uğruna, Dünyanın 24.900 mil çevreyle mükemmel bir küre olduğunu varsayalım.) Şimdi, Dünya’yı yüzeyinin 1 inç uzağında saran bir şerit için gerekli uzunluğu belirlemeye çalışın. İçgüdüsel olarak ikinci şeritin ilk şeritten önemli ölçüde daha uzun olması gerektiğine inanıyorsanız, bu konuda yalnız değisilsiniz ama yanılmış olrsunuz. Aslında, ikinci şerit sadece 2pi veya kabaca 6.28 inç uzunluğunda artacaktır.
Yine, Dünyanın mükemmel bir küre olduğunu varsayarsak, ekvatorda 24.900 mil etrafında dev bir daire olarak düşünülebilir. Bu, yarıçapın 24.900 / 2pi veya kabaca 3.963 mil olacağı anlamına gelir. Şimdi, eklenen ikinci şerit, Dünya yüzeyinin 1 inç üzerinde gezinirken, C = 2 Pi (r + 1) eşdeğeri C = 2 Pi (r + 1) denklemine yol açan, Dünya’nınkinden bir inç daha uzun bir yarıçapa sahip olacaktı. ) + 2 Pi.Bundan, ikinci şerit çevresi 2pi artacağını söyleyebiliriz. Aslında, orijinal yarıçapı ne olursa olsun (Dünya’nın veya basketbolun olsun), yarıçapı bir inç artırırsanız çevrede daima 2pi (sadece 6.28 inç) artış olur.
Pi ve Navigasyon
Pi, özellikle büyük ölçekli küresel konumlandırma söz konusu olduğunda, navigasyonda belirgin bir rol oynamaktadır. İnsanlar, Dünya’ya kıyasla oldukça küçük olduğu için seyahatin doğrusal olduğunu düşünmeye eğilimlidir. Bununla birlikte, uçaklar uçtuğunda tabii ki bir dairenin yayında uçarlar. Bu nedenle uçuş yolu, seyahat süresini, yakıt kullanımını vb. Doğru bir şekilde ölçmek için hesaplanmalıdır. Ek olarak, bir GPS cihazı kullanarak kendinizi Dünya’da bulursanız, pi’nin bu hesaplamalarda önemli bir rol oynaması gerekir.
New York’tan Tokyo’ya giden bir uçuşa kıyasla daha da fazla mesafelerde daha kesin kesinlik gerektiren seyrüsefer ne olacaktı? NASA için Uluslararası Uzay İstasyonu Kılavuz Navigasyon ve Kontrol (GNC) alt sistemi yöneticileri özellikle NASA’nın pi kullandığı hesaplamaların çoğunun 15 veya 16 haneli kullandığını ortaya koyuyor; Uzay Entegre Küresel Konumlandırma için süper kesin hesaplamalar gerektiğinde Sistem / Atalet Seyrüsefer Sistemi (SIGI) – görev sırasında uzay aracını kontrol eden ve stabilize eden programı kullanıyor
Sinyal İşleme Ve Fourier Dönüşümü
Pi, bir dairenin alanının hesaplanması gibi geometrik ölçümler yapmak için en iyi olarak bilinirken, bir sinyali bir frekans spektrumuna çeviren, çoğunlukla Fourier dönüşümü olarak bilinen bir işlem aracılığıyla, sinyal işlemede de belirgin bir rol oynar. Fourier dönüşümü, frekans alanını ve frekans alanını bir zaman fonksiyonuna bağlayan matematiksel işlemi ifade eder, orijinal sinyalin “frekans bölgesi gösterimi” olarak adlandırılır.
İnsanlar ve teknoloji , bir sinyal, temel bir dönüştürmeye ihtiyaç duyduğunda, örneğin iPhone’unuz baz istasyonundan bir mesaj aldığında veya kulağınız farklı zift sesleri arasında ayrım yaparken bu olgudan yararlanır. Fourier dönüşüm formülünde belirgin olarak görülen Pi, Euler’in Sayı’nın (ünlü matematiksel sabitin 2.71828’e eşit olduğu) üslubunda olduğu gibi, dönüştürme sürecinde temel ancak bir hayli gizemli bir rol oynamaktadır.
Normal Olasılık Dağılımı
Pi’nin birincil olarak sinyaller (ve daha sonra dalgalar) ile uğraşan Fourier dönüşümü gibi operasyonlarda bulunması beklenirken, pi’nin normal olasılık dağılımı formülü üzerinde önemli bir rol oynadığını bulmak şaşırtıcı olabilir.Kuşkusuz bu ünlü dağılımdan daha önce rastlamışsınızdır – gördüğümüz geniş bir yelpazede düzenli olarak, zar atmalarından test puanlarına kadar uzanmaktadır.
Pi karmaşık bir denklemde gözüktüğünde , bir daireyi matematiksel bir kumaşın herhangi bir yerinde gizlediğini varsayalım. Normal olasılık dağılımında, pi, pi’nin kareköküne sahip Gauss integrali (Euler-Poisson integrali olarak da bilinir) yoluyla iletilir. Aslında, normal dağılımın normalleştirme sabitini hesaplamak için gereken tek şey, Gauss integralindeki değişkenlerdeki hafif değişikliklerdir.
Gauss integralinin yaygın fakat yine de karşı olmayan bir uygulaması, bir düzlemdeki rüzgar rüzgarlarından büyük ölçekli inşaat sırasında ışın titreşimlerine kadar her şeyi önceden tahmin etmek için kullanılan normal dağılımlı bir rasgele değişken olan “beyaz gürültü” içerir.
Meandering Nehirleri
Pi’nin nehirlerin kıvrımlarıyla büyüleyici ve beklenmedik bir ilişkisi var. Bir nehrin yolu çoğunlukla sinüozitesi ile tanımlanır – bir ovayı geçerken yanlamasına yorulma eğilimi. Bu, matematiksel olarak, sarım yolunun uzunluğu, kaynağından ağzına kadar olan nehrin uzunluğuna bölünmesiyle tanımlanabilir. Nehrin uzunluğuna bakılmaksızın ya da yol boyunca kaç bükülme ve dönüş yaparsa yapsın, ortalama nehir kabaca pi bir sinuoziteye sahiptir.
Albert Einstein nehirlerin bu şekilde davrandıklarına ilişkin birkaç gözlem yaptı . Suyun bir nehrin kıvrımının etrafında daha hızlı aktığını fark etmiş ve etrafında daha hızlı erozyona neden olmuş ve bu da daha büyük bir viraj yaratıyor. Bu daha büyük kavisler ile buluşuyor, nehrin “kısayol” bağlantısı oluşturmasına neden oluyor. Bu geriye-gidiş hareketi, nehrin sinülozu pi’ye geri döndüğünde kendisini sürekli olarak düzeltmektedir.
Pi Ve Fibonacci Dizisi

Pi Ve Fibonacci Dizisi
Tarihin büyük bölümünde, Archimedes tarafından icat edilen pi’yi hesaplamak için yalnızca iki yöntem vardı ve diğeri İskoç matematikçisi James Gregory tarafından yapıldı.
Bununla birlikte, pi’nin Fibonacci dizisi kullanılarak hesaplanabileceği çıkar. Fibonacci dizisindeki her sonraki sayı önceki iki sayının toplamıdır. Sıra 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 ile başlar ve sonsuza kadar devam eder. Ve 1’in arkctentini pi / 4 olduğu için, pi’nin denklemi arctan (1) * 4 = pi olarak yeniden düzenleyerek, pi’nin Fibonacci sayılarıyla ifade edilebileceği anlamına gelir .
Doğal olarak büyüleyici ve güzel bir sayı dizisine sahip olmanın yanı sıra, Fibonacci dizisi, kozmosun her yerinde çeşitli doğal hadiselerde önemli bir rol oynamaktadır. Matematik ve bilim, sanat ve doğada inanılmaz bir fenomen modeli ya da açıklayabilir. Altın oran, spiraller ve eğriler gibi Fibonacci dizisinin yol açtığı matematiksel düşünceler, güzelliği için uzun zamandır takdir edilmekle birlikte, matematikçiler hala bağlantı derinliğini açıklamaya çabalıyorlar.
Kuantum Mekaniği
Pi, şüphesiz, dünyamızın kaçınılmaz ve karmaşık bir temelidir, fakat genel olarak evren ne olacak? Pi kendini evrenin her yerinde tezahür eder ve evrenin doğasını açıklamak isteyen denklemlerde gerçekten yer alır. Nitekim atomların ve çekirdeklerin mikroskobik dünyasını yöneten kuantum mekaniği alanında kullanılan pek çok formül pi’yi kullanır .
Belki de bu tür denklemlerin en ünlüleri, Albert Einstein’ın alan denklemleri (aynı zamanda Einstein’ın denklemleri olarak da bilinir); Einstein’ın genel görelilik teorisinde, kütlenin eğri uzay-zamanının bir sonucu olarak çekim gücünün temel etkileşimini tanımlayan 10 denklem kümesidir Ve enerji. Bir sistemde bulunan yer çekimi miktarı, enerji ve momentum ile orantılıdır; orantılılık sabiti, sayısal sabit olan G’ye bağlıdır.